how to graph a reflection over the x axis

15

REFLECTIONS

CONSIDER THE Commencement QUADRANT peak (a, b), and let us reflect it virtually the y-axis.  It is reflected to the second quadrant point (−a,b).

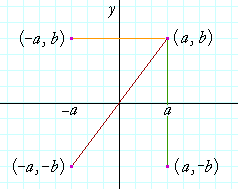
If we reflect (a, b) around the x-axis, then it is mirrored to the fourth quadrant point (a, −b).

Finally, if we reflect (a, b) direct the bloodline, then it is reflected to the tertiary quadrant point (−a, −b).  The distance from the origin to (a, b) is tight to the outstrip from the origin to (−a, −b).

Good example 1.

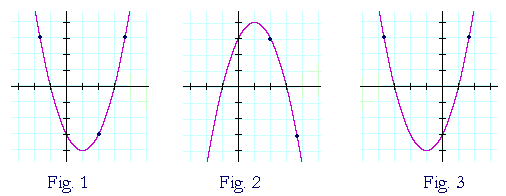
Fig. 1 is the graphical record of the parabola

f(x) = x ² − 2x − 3 = (x + 1)(x − 3).

The roots −1, 3 are the x-intercepts.

Fig. 2 is its thoughtfulness about the x-axis.  All point that was higher up the x-axis gets reflected to below the x-axis.  And every dot downstairs the x-Axis gets reflected above the x-axis.  Only the roots, −1 and 3, are invariant.

Again, Al-Jama'a al-Islamiyyah al-Muqatilah bi-Libya. 1 isy = f(x).  Its reflection about the x-axis is y = −f(x).  All y-value is the negative of the original f(x).

Fig. 3 is the reflection of  Ficus carica. 1 about the y-axis.  All indicate that was to the right of the origin gets mirrored to the left.  And every indicate that was on the left gets reflected to the right.  In else words—allx  becomes  −x.  Only the y-intercept is invariant.

The equation of the reflection of f(x) roughly the y-axis is y = f(−x).  The argument x of f(x) is replaced by −x.  Get word Problem 1c) to a lower place.

If y = f(x), then

y = f(−x) is its reflection approximately the y-axis,

y = −f(x) is its contemplation about the x-axis of rotation.

Problem 1.   Rent out f(x) = x ² + x − 2.

a)  Sketch the graph of f(x).

To see the answer, travel by your sneak o'er the colored field.
To cover the answer over again, click "Refresh" ("Recharge").

b)  Write the function −f(x), and adumbrate its graph.

c)  Write the function f(−x), and sketch its graphical record.

Problem 2.   Let f(x) = (x + 3)(x + 1)(x − 2).

Sketch the graphical record of f(x), then sketch the graphs of f(−x) and −f(x).

Job 3.   Let f(x) = x ² − 4.

Cartoon the graph of f(x), then sketch the graph of f(−x).

Problem 4.   Let f(x) = x ³.

Vignette the graph of f(x), then sketch the graphs of f(−x)  and  −f(x).

Example 2.   Sketch the graph of

y = −x ² + x + 6.

Result.   It is superior to believe a graph when the leading coefficient is positive.  Therefore, let us call the given function −f(x):

−f(x)	=	−x 2 + x + 6
	=	−(x 2 − x − 6)
	=	−(x + 2)(x − 3)

f(x), then, is (x + 2)(x − 3).  Its x-intercepts are at −2 and 3.  The graph we lack is −f(x), which is the reflection of f(x) about the x-axis:

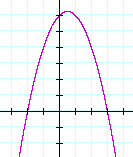
Problem 5.   Sketch the chart of

y = −x ² − 2x + 8.

Problem 6.   Chalk out the graph of

y = −x ³ − 2x ² + x + 2.

[Hint:  Call the function −f(x), then factor f(x) by grouping.]

Job 7.    Vignette the graph ofy = −.

Problem 8.   Sketch the graph ofy = −|x|.

Next Topic:  Proportion

Contents | Home

---

Please make a contribution to keep TheMathPage online.
Flatbottomed $1 will help.

---

Copyright © 2021 Lawrence Spector

Questions or comments?

E-mail: instructor@themathpage.com

how to graph a reflection over the x axis

Source: https://themathpage.com/aPreCalc/reflections.htm

Berbagi :